报告题目：Cesàro summability of noncommutative Vilenkin-Fourier series
报告人：赵甜甜 博士
工作单位：哈尔滨工业大学
报告时间：2025年01月21日 09:00-11:00
报告地点：哈哈体育 305
报告摘要：
We study several noncommutative asymmetric maximal inequalities for the Cesàro means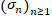 
of the Vilenkin-like-Fourier series of functions in 
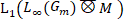, where 
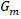is a Vilenkin space and 
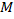is a semifinite von Neumann algebra. Vilenkin-like system is a common generalization of the Walsh system, Vilenkin system, the character system of the group of 2-adic (m-adic) integers and other systems. When focus on the Vilenkin system, we transfer the above inequalities into totally noncommutative case for the Cesàro means 
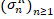of the noncommutative Vilenkin-Fourier series in the hyperfinite 
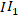factor 
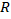. The primary strategy in our proof is to explore a noncommutative generalization of Sunouchi square function operator, and the very recent advance of the noncommutative Calderón-Zygmund decomposition established by Cadilhac, Conde-Alonso and Parcet.
This is a joint work with Yong Jiao, Sijie Luo and Dejian Zhou.
报告人简介：
赵甜甜，博士，泛函分析与非交换分析方向。2023年毕业于中南大学数学与统计学院，导师为焦勇教授。现为哈尔滨工业大学数学研究院博士后。研究主要集中于泛函分析和非交换分析领域，具体包括算子值的调和分析问题和函数空间问题。
欢迎广大师生莅临交流学习！
